3.21 FAQ-247 Why is R-Square greatly different when intercept is fixed in linear fit?R-Square-in-Fixed-Intercept
Last Update: 2/26/2020
Why is R-Square greatly different when intercept is fixed in linear fit?
It is because the R-Square is calculated with equation below:
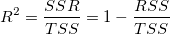
where SSR is the sum of squares due to regression, TSS is the total sum of squares, and RSS is the residual sum of squares. For TSS:
-
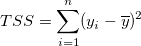 , when intercept is not fixed , when intercept is not fixed
-
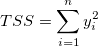 , when intercept is fixed , when intercept is fixed
| Notes:
Excel uses the corrected TSS , the first equation above to calculate the R-Square no matter the intercept is fixed or not. If you compare the linear fit result of Origin and Excel, you will find R2 is very different.
|
Please look at the detailed explanation below why we use uncorrected sum of squares for TSS calculation when intercept is fixed.
When intercept is fixed
When intercept is fixed in linear fit, it follows the relation below:
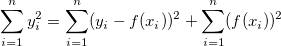
Then TSS and SSR need be redefined, and RSS is unchanged.

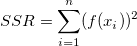
And the coefficient of determination (R-Square) is redefined as follows:
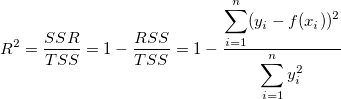
Please refer to Additional Information of R-square chapter for more information.
Keywords:linear fit, R-Square, intercept, fixed
|